Marketing companies use the market response to price products, determine advertising expenditures, forecast sales or prepare and test the effectiveness of various marketing plans and campaigns. Predictions of future traffic for online marketing campaigns can be based on data analysis and market response models. Mathematical models have become the main tools for marketing decision-making. The main goal of this paper is to describe and show how to use behavioral modelling of potential customers in online marketing campaigns. In addition to the basic ARMA model for short-term website traffic forecasting, we evaluate the TBATS and Prophet models. Both models comprehensively capture seasonal and holiday fluctuations. More specifically we show how time series modelling can be incorporated into the evaluation of online marketing campaign traffic forecasts for marketing agency clients.
1 Introduction
The ever-increasing internet connectivity creates global changes not only in strategic but also in marketing thinking. New technological tools affect our lives and thereby deepen our dependence on the Internet. Technologies have made some activities easier for us, for example ordering food or shopping. Many experts advise how to become visible in the Internet markets by creating a suitable online marketing campaign for their clients. The reason these experts are needed is because of the Google search engine. Google’s main algorithms hide and analyze data published on websites. A website builder for an online marketing campaign creates links that must be of high quality and must link the content of the website together with the content that the link links to. Ideally, this page should be an authority such as Quora, LinkedIn, or other publishing platforms. Google evaluates these links and notes the extent to which it can trust them (Monti 2021), (Park 2022), (Slawski 2012), (Chawla and Chodak 2021), etc. If a website gains Google search engine’s trust, it will more easily increase its traffic and visibility on the Internet.
This paper aims to show how to evaluate and influence online marketing campaigns using data evaluation with mathematical-statistical models. Using an example of two clients, we show possible scenarios of how to achieve the client’s marketing goals for its operation on the market based on the analysis of available data and the services we provide to the client.
The paper is organized as follows. After the literature review, we introduce the used methods to evaluate the traffic of online marketing campaigns. We then present our results and summarize the paper as part of the conclusion.
2 Literature review
The effectiveness of online marketing campaigns is a topic that is important not only for entrepreneurs and their marketers but also for researchers. Many studies apply forecasting methods to predict the traffic and success of online marketing campaigns. Forecasting traffic of the websites is critical for planning, production and investment strategies. Many authors use time series models such as short-term autoregressive moving average (ARMA) models (Box and Jenkins 1976), Exponential smoothing models, and Holt-Winters models (Cipra 2020). ARMA models represent an important method for investigating time series while achieving a small prediction error. ARMA models can be applied to stationary stochastic processes. Traffic time series often show systematic upward or downward trends and cyclical fluctuations. Such time series should be modelled with the TBATS model (Munim 2022), (Naim et al. 2018), (De Livera et al. 2011) which generalizes the Holt-Winters smoothing model that is used when a single seasonal pattern is present. Another approach is offered by the Prophet model introduced by Facebook’s Core Data Science team (Guo et al. 2021), (Zhao et al. 2018). We propose to evaluate the traffic of online marketing campaigns using the above methods.
3 Methodology
The main contribution of this paper is to explain how we can use time series models in online marketing campaigns. The first step to evaluating an online marketing campaign is to set campaign goals and quantifiable metrics. The value of the quantifiable metrics must be determined usually once a month. It can be either a fixed number based on data, according to the client’s request, or a percentage change compared to a certain period, usually year-on-year or month-on-month. Online marketing campaign goals can be different. We present here the most common campaign goals:
• Turnover – total value of the orders that the campaign achieves (typical for e-shops)
• Conversion rate – the ratio between visits to the site and purchases, i.e. if one of the 100 people who came to the website buys, the conversion rate is 1%
• Spent credit – for paid campaigns
• ROAS – return on ad spend – the ratio between turnover and credit, if the campaign earns 100 Euro and 100 Euro is spent on it, ROAS is 100% and the client is at imaginary zero
• Traffic on the site
• Micro-conversions – they are interesting mainly in the case of sites that are not e-shops
1. Number of submitted forms
2. Clicking on a contact
3. Document download
• Bounce rate – if a visitor comes to the site and immediately leaves without any interaction, it is counted in the bounce rate. The bounce rate tells you what percentage of visits are bounced. If the bounce rate is 35%, we can interpret it as 35 bounces out of 100 visits to the website.
• Any other calculated metric – a combination of several metrics.
Another important step is to determine which sources will fulfil the selected goals. If we want to increase paid traffic, we can use AdWords. If the goal is to increase organic traffic, then we can improve search engine optimization (SEO). Social media can also be a source that can help us achieve the selected goals.
The attribution model (Kannan et al. 2016) plays a large role in paid traffic. Attribution models determine how different channels are given credit for accomplishing goals. Consider the following situation:
1. A customer sees a banner ad, then sees an ad on Facebook, clicks on it and learns about the product.
2. Then searches for the product and uses a paid ad to enter the site, but does not buy the product at this stage.
3. Remembers the name of the site, writes it directly and purchases.
Which channel should be credited? Is it the banner ad because it was the first? Or Facebook because the customer clicked on that first? Or the paid ad because it was the closest to when the customer bought the product? They all have merits in their ways. Google Analytics uses the following attribution models (Slawski 2012), (Anderl et al. 2016):
• Last interaction – the whole weight is attributed to the last channel.
• Last, Non-Direct Click – the whole weight is attributed to the last channel, except for a direct visit.
• Last AdWords Click – the whole weight is attributed to AdWords if it is in the conversion path.
• First interaction – the whole weight is attributed to the first interaction.
• Linear – the weight is distributed evenly among all channels in the conversion path.
• Time Decay – the weight is distributed among all channels, the latest channel has the most weight, and the earliest the least.
• Position Based – the weight is distributed so that the first and last interaction have the largest weight.
• Data-driven – based on data, but available only for relatively large amounts of data, which is not the norm. This is supposedly the best model.
• Custom models – the Markov model, based on probability, is often used.
The last step is the selection of a suitable model that will allow us to predict the traffic of online marketing campaigns. Online marketing campaign traffic estimations often use ARMA models.
ARMA model
The ARMA model relates observations about current traffic online marketing campaigns to previous traffic observations and previous shocks. AR models have infinite memory while the strength of the contribution varies with p. Moving average models have a finite memory of order q. A critical question is how to identify the parameters p and q of the ARMA model of a given series (Hanssens et al. 2005). ARMA model is composed of AR and MA models.
AR model is expressed as
![]()
where ![]() are models parameters, c is a constant term and
are models parameters, c is a constant term and ![]() is an error term that follows the Gaussian white noise process.
is an error term that follows the Gaussian white noise process.
The MA model is expressed as
![]()
where ![]() are the model parameters, μ is the expected value of
are the model parameters, μ is the expected value of ![]() and random variables
and random variables![]() represent error terms as white noise.
represent error terms as white noise.
Finally ARMA model combines both AR and MA models:
![]()
ARMA models can be used to assess which conditions hold in a marketing online campaign: stationarity (mean-reverting) behaviour or evolving (ever-changing) behaviour (Hanssens et al. 2005).
If the traffic of an online marketing campaign has a rapid surge in sales performance, the question is if that increase is temporary (short-run) or permanent (long-run). Therefore Unit-root tests (Cipra 2020) are used to identify the presence of a long-run or stochastic-trend component in a traffic data series. In the absence of a unit root, all observed fluctuations in an online marketing campaign performance or marketing support are temporary deviations from a deterministic component (such as a fixed mean or a deterministic trend). With a unit root, the traffic time series may move widely apart from any previously held position.
Although the ARMA models are widely used, we propose to use either the TBATS models which use exponential smoothing and incorporates multiple seasonal patterns or the Prophet model.
TBATS model
TBATS model was introduced by De Livera et al. (2011). This model combines multiple seasonal periods, high-frequency seasonality, non-integer seasonality and dual calendar effects. In the TBATS model (De Livera et al. 2011), (Munim 2022), (Naim et al. 2018), T means trigonometric terms for seasonality, B stands for Box-Cox transformation to heterogeneity, A describes ARMA errors to explain short-term dynamics, T determines the trend, and S denotes seasonal term.
TBATS model includes Box-Cox transformation:
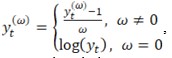
seasonal periods component:

the global and local trend:
![]()
ARMA errors:
![]()
where ![]() represents Box-Cox transformation for parameter ω,
represents Box-Cox transformation for parameter ω, ![]() is the local level in time t,
is the local level in time t,![]() is the short-term trend in time t,
is the short-term trend in time t, ![]() is the trend damping parameter,
is the trend damping parameter, ![]() denotes the i-th seasonal component at time t,
denotes the i-th seasonal component at time t, ![]() refer to seasonal periods, dt represents an ARMA (p, q) process and
refer to seasonal periods, dt represents an ARMA (p, q) process and ![]() is a Gaussian white noise process with zero mean and constant variance σ2. α, β are smoothing parameters for i = 1, …, T. ki denotes the required number of harmonics for the i-th seasonal component.
is a Gaussian white noise process with zero mean and constant variance σ2. α, β are smoothing parameters for i = 1, …, T. ki denotes the required number of harmonics for the i-th seasonal component.
Fourier seasonal terms are expressed as

![]() and
and ![]() are smoothing parameters.
are smoothing parameters. ![]() is the stochastic level of i-th seasonal component.
is the stochastic level of i-th seasonal component. ![]() is the change in the stochastic level of the i-th seasonal component during the analyzed period.
is the change in the stochastic level of the i-th seasonal component during the analyzed period.
The Prophet model
The Prophet model was introduced by Taylor and Letham (2018). The Prophet model should be compared with Holt-Winters and ARIMA models, but it uses a Bayesian-based curve fitting method to smoothen and forecast given time series (Zhao et al. 2018), (Guo et al. 2021). The Prophet model was proposed to discover holidays and seasonality in time series. Moreover, this model considers large trend changes based on daily, weekly, monthly, quarterly, and annual data and is appropriate to use for periodic time series data with many outliers.
The Prophet model is available within an open-source library (Munim 2022) that can achieve impressive performance with simple and intuitive parameters and can consider the influence of seasons and holidays.
The Prophet model introduced by Taylor and Letham (2018) can mathematically be expressed as
![]()
where y(t) is the forecasted value obtained by the model; g(t) is the trend function, which determines nonperiodic changes in the time series values; s(t) is the periodical function, influenced by weekly and yearly seasonality; and h(t) represents the effect of holidays for various periods. The error term ![]() is used to represent abnormal changes that are not reflected by the model which follows a normal distribution.
is used to represent abnormal changes that are not reflected by the model which follows a normal distribution.
The trend function g(t) can be either a piecewise linear function expressed as (Guo et al. 2021)
![]()
or a logistic function expressed as
![]()
where C(t) is a time-varying parameter or the non-constant carrying parameter; k is the growth rate; δ is the vector of rate adjustments of the growth rate; γ is the vector of correction adjustments at change points or trend change point; α(t) is the vector of adjustment parameters, and m is an offset parameter. The optimal model parameters are estimated using the grid search with the cross-validation method.
The seasonal effects are modelled by a Fourier series:
![]()
where N is the number of cycles of the model; P represents the length of the period of the given time series; 2n is the number of parameters that must be estimated to fit seasonality; an is the amplitude of the cosine function of the frequency doubling of n and bn is the amplitude of the sinusoidal frequency doubling of n. P is equal to 365.25 for annual data and P is equal to 7 for weekly data.
Holidays or major events can cause unpredictable fluctuations in the traffic time series. To avoid these unpredictable fluctuations, matrices containing the dates and details about holidays are prepared.
4 Results
We show how to evaluate the traffic of online marketing campaigns for clients of an agency providing implementation of marketing online campaigns. The client sets one or more goals that they want to achieve with the help of an online marketing campaign.
We will evaluate the online marketing campaign based on the analysis of data obtained from Google Analytics.
Consider a client who offers DIY materials in his e-shop. Let’s assume that the e-shop is well established and brings the owner a profit comparable to their brick-and-mortar store. We provide PPC (Pay-per-click) services to the client and therefore focus only on campaign results, specifically monitoring ROAS metrics and campaign traffic. An overview of the campaign’s metrics is presented in Table 1:
| Target ROAS | 200% | Actual ROAS | 715.49% |
| Target spend | 1500 EUR | Actual spend | 1248.22 |
| Target transaction revenue | 3000 EUR | Actual transaction revenue | 8930.88 |
Table 1: Overview of client metrics for PPC service
Source: Křížková (2018)
The campaigns follow the set goals and surpass them as can be seen in Table 1. The main reason is that the campaigns are focused on performance, which means that the keywords are so-called „longtails“. A longtail is a multi-word keyword and indicates that the searcher already knows almost exactly what they need. A potential customer is already close to making a purchase when they enter a specific keyword into the search engine.
Moreover for this client, we monitor the traffic that we bring to the e-shop through paid advertising. When deciding how to effectively measure traffic, we concluded that a month-to-month comparison was not appropriate due to the seasonality of the product. A year-on-year comparison came into consideration, but it also has limitations because it would be enough for us to have achieved a better result than the same month a year ago. Another possibility is to set a certain percentage of growth and try to meet it. For example, set a goal to bring 20% more traffic to the e-shop compared to last year. However, the question remains how to set this growth. If we set it too low, we will not use the full potential of the campaign. If we set it too high, we will be trying for the impossible and will not meet the goal. So we decided to use time series analysis, specifically the Prophet model. The first advantage is already mentioned in the monthly goal setting, and the second advantage is the ability to check in real-time whether the traffic behaves as expected. At some point the set credit for paid ads runs out and the ads stop showing. The traffic from paid ads will then drop to zero.
Actual short-term period daily traffic data is shown as the black line, and predicted traffic data is shown as the blue line in Figure 1. The grey band represents the confidence intervals. The decrease in the last recorded point of real traffic (in the middle of the graph) is caused by using data only up to the morning of that day.
Figure 1: Traffic graph and traffic prediction using the Prophet model, short-time period
Source: Křížková (2018)
The long-term period for traffic data is shown in Figure 2.

Figure 2: Traffic graph and traffic prediction using the Prophet model, long-time period
Source: Křížková (2018)
It is advisable to recalculate the traffic forecast daily. If there were significant changes in the campaign, the prediction would have to be adjusted. This would not be possible if we calculated the prediction only once.
This approach is suitable for clients with a long history of online campaigns, as it can detect seasonality and take it into account for the forecast. Figure 3 shows the decomposition of the 3 trends. The first graph in Figure 3 shows the trend over the years. The second chart shows the trend over the days of the week and the last chart shows the trend over the months of the year. The last graph is interesting because it shows the client when there is the season and when there is a slump. This information should be useful for allocating money in advertising because it is worth investing more money in paid advertising during the starting season compared to the off-season. We can automatically raise the maximum price per click on days when there is a higher buying potential, specifically in this case it would be Sunday and Monday as is seen from the second graph. The first graph is a good indicator that the campaigns are doing well. If the trend had a downward character, it would be a sign that the specialist working on these campaigns needs to make drastic changes to ensure an increasing trend.

Figure 3: Model Prophet and the trends
Source: Křížková (2018)
Another client sells parts for motor vehicles. SEO optimization is carried out for this client. The client’s goal is to increase organic/unpaid traffic to its website by 20% compared to last year. In Table 2, we see the estimate of organic/unpaid traffic growth determined by the Prophet model. We see the estimate and the real situation differ.
| Target value / Organic sessions | +20% YoY 13939 | Actual value / Organic sessions | 21475 |
| Prophet prediction for the actual month | 21583.28 | Actual value | 21475 |
Table 2: Overview of client metrics with SEO optimization
Source: Křížková (2018)
Let us look at Figure 4. Figure 4 shows a graph of the organic search traffic for the monthly frequency of the data. The black colour line shows the real daily values, the blue line is the Prophet model prediction and the grey band is the confidence interval corresponding to the Prophet model. We can see some spikes in traffic that fall outside of these confidence intervals and therefore we look at the detailed part of this graph, which is shown in Figure 5.

Figure 4: Traffic graph and prediction using the Prophet model, monthly (medium) period
Source: Křížková (2018)

Figure 5: Traffic graph and prediction using the Prophet model, daily (short) period
Source: Křížková (2018)

Figure 6: Traffic graph and prediction using the Prophet model, yearly (long) period
Source: Křížková (2018)
The reason for the observed traffic behaviour on the website is as follows. The client decided to turn off paid advertising at the beginning of March, which led to an increase in visits from organic traffic and therefore falls outside the confidence interval. We will now explain why there was a big difference in the targets created using the year-over-year comparison and using the Prophet model. In the previous year, paid advertising was not turned off, and therefore it was not possible to estimate the change in traffic using percentage growth. If paid advertising had not stopped in March, the percentage growth model may have been more reliable. However, the Prophet model has noticed this change, although it is not yet perfectly visible in the daily data (Figure 5). The monthly forecast is getting closer to reality (Figure 4). However, when we display the entire available data period (Figure 6), this increase is more obvious.
Now we compare the results obtained by the Prophet model with other models. Figure 7 shows the prediction of the organic search traffic for the monthly frequency of the data using Exponential smoothing, ARIMA and TBATS models. Akaike Information Criterium AIC (Cipra 2020) was used to select the appropriate model. It turned out that the Prophet model was the best in being able to respond to changes in the client’s online campaign settings.
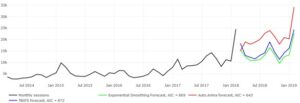
Figure 7: Traffic graph and prediction using Exponential smoothing model, ARIMA and TBATS model
Source: Křížková (2018)
5 Conclusion
Online marketing traffic is very dynamic, so both researchers and marketing managers actively look for new ways to help businesses establish themselves in online markets. At the same time, they try to use scientific knowledge to analyze the behaviour of customers visiting online markets. The ability to predict customer traffic using time series analysis is highly useful for optimizing and setting the strategy of individual campaigns. Our study contributes to the existing scientific literature by providing practical insights obtained from two online marketing campaigns. The paper provides the reader with an insight into the evaluation of online marketing campaign traffic using time series analysis. We suggested using the Prophet and TBATS models to model the traffic of online campaigns. The Prophet model has proven to be the best in responding to changes and predicting traffic for online marketing campaigns.
Poznámky/Notes
The first author kindly announces the support of the KEGA 029UKF-4/2022.
Literatúra/List of References
- Anderl, E., Becker, I., von Wangenheim, F., and Schumann, J. H., 2016. Mapping the customer journey: Lessons learned from graph-based online attribution modelling. In: International Journal of Research in Marketing. 2016, 33(3),457-474. ISSN 0167-8116. [online]. [cit. 2023-02-20]. Available at: <https://doi.org/10.1016/j.ijresmar.2016.03.001>
- Box, G. E. and Jenkins, G. M., 1976. Time series analysis. Forecasting and control. Holden-Day Series in Time Series Analysis. Revised ed., San Francisco: Holden-Day, 1976. ISBN 9780816211043.
- Cipra, T., 2020. Time series in economics and finance. Springer, 2020. ISBN 978-3-030-46347-2. [online]. [cit. 2023-02-20]. Available at: <https://doi.org/10.1007/978-3-030-46347-2>
- Chawla, Y. and Chodak, G., 2021. Social media marketing for businesses: Organic promotions of web links on Facebook. In: Journal of Business Research. 2021, 135(October), 49-65. [online]. [cit. 2023-02-20]. Available at: <https://doi.org/10.1016/j.jbusres.2021.06.020>
- De Livera, A. M., Hyndman, R. J. and Snyder, R. D., 2011. Forecasting time series with complex seasonal patterns using exponential smoothing. In: J. Am. Stat. Assoc. 2011, 106(496), 1513-1527. ISSN 0162-1459.
- Guo, L., Fang, W., Zhao, Q., and Wang, X., 2021. The hybrid PROPHET-SVR approach for forecasting product time series demand with seasonality. In: Computers & Industrial Engineering. 2021, 161(107598). ISSN 0360-8352. [online]. [cit. 2023-02-20]. Available at: <https://doi.org/10.1016/j.cie.2021.107598>
- Hanssens, D. M., Parsons, L. J. and Schultz, R. L., 2005. Market response models. Econometric and time series analysis. New York: Kluwer academic publishers, 2005. ISBN 978-0-306-47594-8.
- Kannan, P. K., Reinartz, W. and Verhoef, P. C., 2016. The path to purchase and attribution modelling: Introduction to the special section. In: International Journal of Research in Marketing. 2016, 33(3), 449-456. ISSN 2349-0314.
- Křížková, M., 2018. Online marketing campaigns, their analysis, processing and evaluation. Master thesis, Comenius University Bratislava. Supervisor: Bohdalová, M.
- Monti, R., 2021. Does content or links improve trust with Google? 2021. [online]. [cit. 2023-01-20]. Available at: <https://www.searchenginejournal.com/trust-metrics-and-google/424679/>
- Munim, Y. H., 2022. State-space TBATS model for container freight rate forecasting with improved accuracy. In: Maritime Transport Research. 2022, 3(100057). ISSN 2666-822X. [online]. [cit. 2023-01-20]. Available at: <https://doi.org/10.1016/j.martra.2022.100057>
- Naim, I., Mahara, T., and Idrisi, A, R., 2018. Effective short-term forecasting for daily time series with complex seasonal patterns. In: Procedia Computer Science. 2018, 132, 1832-1841. International conference on computational intelligence and data science (ICCIDS 2018). [online]. [cit. 2023-01-20]. Available at: <https://doi.org/10.1016/j.procs.2018.05.136>
- Olsavsky, F., 2020. Consumer literacy and honey fraud. Part I. In: Marketing Science & Inspirations. 2020, 15(4), 46-51. ISSN 1338-7944. [online]. [cit. 2023-01-20]. Available at: <https://doi.org/10.46286/msi.2020.15.4.5>
- Olsavsky, F., 2021. Consumer literacy and honey fraud. Part II. In: Marketing Science & Inspirations. 2021, 16(1), 2-10. ISSN 1338-7944. [online]. [cit. 2023-01-20]. Available at: <https://doi.org/10.46286/msi.2021.16.1.1>
- Park, J., 2022. Understanding how Google generates title links & what it means for SEO. 2022. [online]. [cit. 2023-01-20]. Available at: <https://cmimediagroup.com/resources/understanding-how-google-generates-title-links-what-it-means-for-seo/>
- Slawski, B., 2012. Google link analysis methods that might have changed? 2012. [online]. [cit. 2023-01-20]. Available at: <https://www.seobythesea.com/2012/03/12-google-link-analysis-methods/>
- Taylor, S. J. and Letham, B., 2018. Forecasting at scale. In: The American Statistician. 2018, 72(1), 37-45. ISSN 0003-1305. [online]. [cit. 2023-01-20]. Available at: <https://doi.org/10.1080/00031305.2017.1380080>
- Vilcekova, L., 2010. Sample size design in marketing research. In: Marketing Science & Inspirations. 2010, 5(2), 23-25. ISSN 1338-7944.
- Zhao, N., Liu, Y., Vanos, J. K. and Cao, G., 2018. Day-of-week and seasonal patterns of PM2.5 concentrations over the United States: Time-series analyses using the prophet procedure. In: Atmospheric Environment. 2018, 192, 116-127. ISSN 1878-2442.
Kľúčové slová/Key words
ARMA model, Prophet model, seasonality, holidays, online marketing
ARMA model, Prophet model, sezónnosť, sviatky, online marketing
JEL klasifikácia/JEL Classification
C10, C22, M31, M37
Résumé
Krátkodobé a sezónne modely časových radov pre online marketingové kampane
Marketingové spoločnosti využívajú odozvu trhu na oceňovanie produktov, určovanie výdavkov na reklamu, prognózovanie predaja či prípravu a testovanie účinnosti rôznych marketingových plánov a kampaní. Predpovede budúcej návštevnosti pre online marketingové kampane môžu byť založené na analýze údajov a modeloch odozvy trhu. Hlavnými nástrojmi marketingového rozhodovania sa stali matematické modely. Hlavným cieľom tohto príspevku je popísať a ukázať, ako využiť modelovanie správania potenciálnych zákazníkov v online marketingových kampaniach. Okrem základného modelu ARMA pre krátkodobé predpovedanie návštevnosti webových stránok hodnotíme modely TBATS a Prophet. Oba modely komplexne zachytávajú sezónne výkyvy a výkyvy spôsobené sviatkami alebo dovolenkami. Konkrétnejšie ukážeme, ako možno modelovanie časových radov začleniť do vyhodnocovania prognóz návštevnosti online marketingových kampaní pre klientov marketingových agentúr.
Recenzované/Reviewed
10. March 2023 / 22. March 2023












